3 つの 連立 方程式 の 解き方 226700

連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト

連立方程式の解き方 (加減法1) 連立方程式は文字が2つあるので、どちらかの文字を消して文字1つの方程式として解く x,yのうちどちらかの係数をそろえて、2式を「たす」または「ひく」かして文字を1つ消す方法を加減法という。 係数が同じなら引き算し、絶対値が同じで符号が違うだけならそのまま足し算する。 yの係数が3と3なので、そのまま足せばyが消える 「10の位は、1の位の数以外の数であるから決め方は4通りある」の意味がわかりません。 問題文 2から6までの自然数が書かれている5個のたまを袋に入れて、よくかき混ぜてから1個ずつ2回続けてたまを取り出す。 最初に取り出した玉の数字を10の位の、あとに取り出したたまの数を1の

3 つの 連立 方程式 の 解き方

3 つの 連立 方程式 の 解き方-連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さ もうすぐ中間テストがあって、今数学を勉強しているのですが 3つ式がある場合の連立方程式の解き方が分かりません。 中学校で習った記憶はあるのですが、どうしても思い出せず、ネットで調べてみても出ませんでした。 A：～ B：～ C：～ この様にA

連立方程式 3つの文字 式の問題を計算する方法は 数スタ

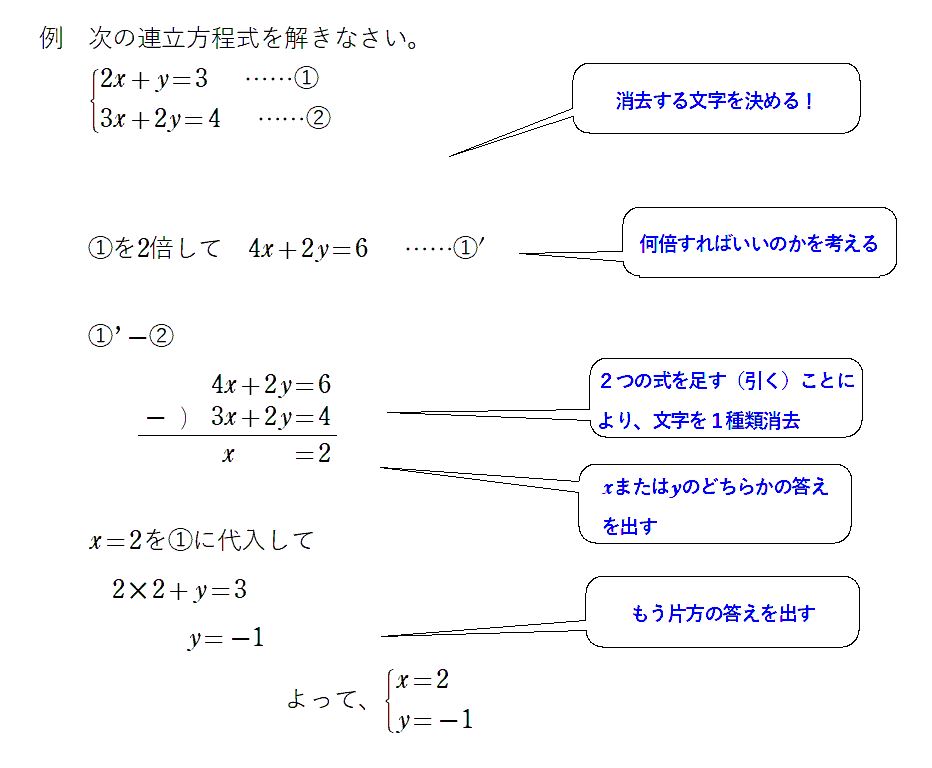
 連立方程式の解き方をみわける2つのコツ 連立方程式の解き方（加減法or代入法）を見分けるコツは、 代入法で解く特殊なケースを覚える ってことさ。 これを覚えちゃえば、 特殊なケースに出くわしたら「代入法」、 ソレ以外は「加減法」で解けるよね！3 式にかっこが含まれる連立方程式の解き方 31 例\begin{eqnarray}\left\{\begin{array}{l}x3y=7\\2(x2y1)y=3\end{array}\right\end{eqnarray} 4 頻出連立方程式の係数が分からない問題の解き方連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に 加減法 と 代入法 がある。 加減法 x,またはyの係数をそろえて2つの式を 「たす」または「ひく」して文字を一つ消す。 加減法のときは式を2つとも ax by = 定数 の形に整理する。 係数の絶対値が等しい場合 係数の絶対値が等しく符号も同じなら引き算し、絶対値が等しくて符号が違うだ

 連立方程式でy＝4という数字がでて x²＋y²=25 x=2y＋5 のどちらかに代入すればx=3という数字がでて正解なのですが、僕が習った知識だとどちらに代入しても答えは一緒なんですが、答えが3と3で変わってしまいます。この場合下の式に代入すれば3で正解なのですが、下の式じゃなきゃダメなのこの問題では(2)を2倍すると y の係数がそろいますので、引き算により y が消去できて x だけの方程式になります。 →(3) (3)の結果を(1)か(2)のどちらかに代入すると、もう一つの未知数も求まります。 ここまでの線形代数シリーズでは、逆行列・行列式・行列の演算などを紹介してきました。 今回は、それらを使って基礎的な連立方程式を解く方法を解説します。 ここでは二元一次連立方程式を扱いますが、これは次回以降の3元1次（3×3）の基本となる部分なので、しっかりと流れを習得しておきましょう。 （続編完成しました：「 3×3行列とサラスの公式

3 つの 連立 方程式 の 解き方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

連立３元１次方程式 身勝手な主張	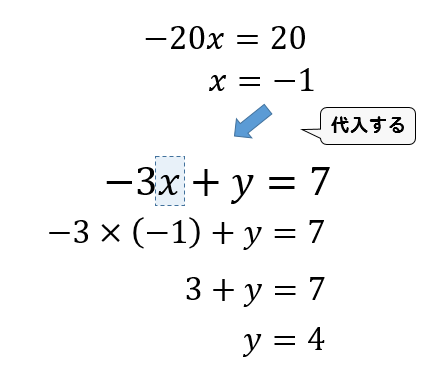連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	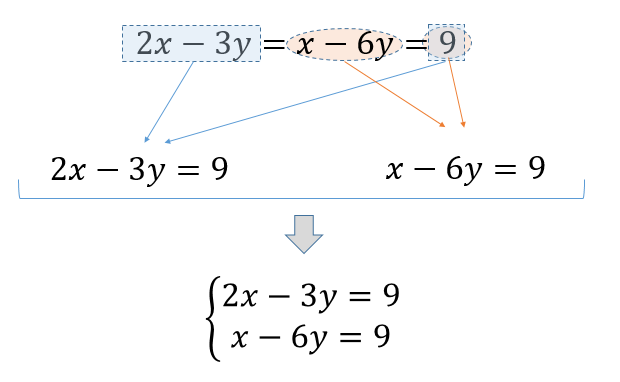連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
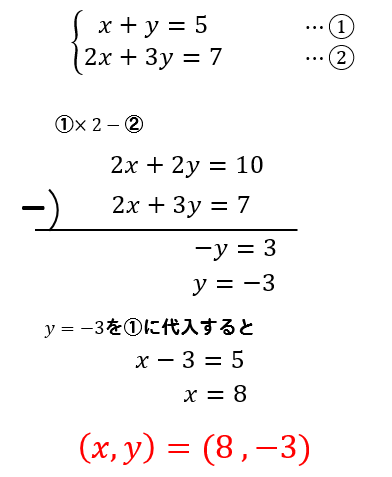連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	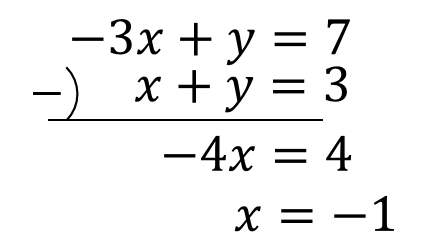連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	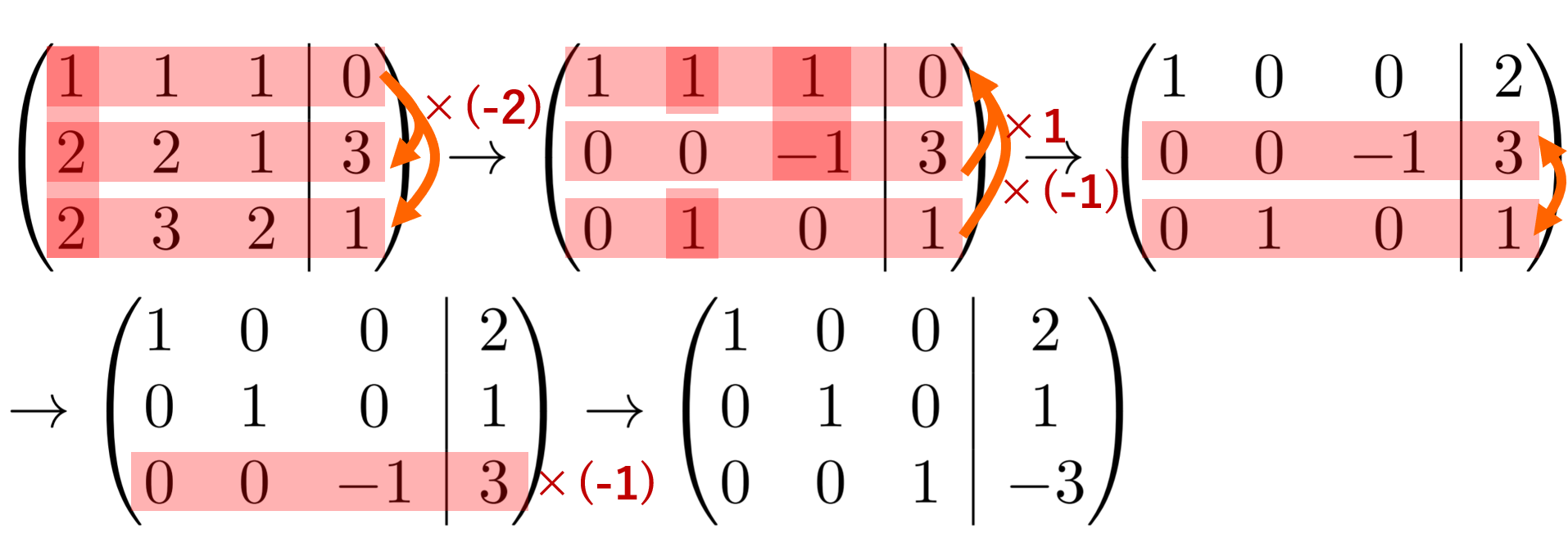連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	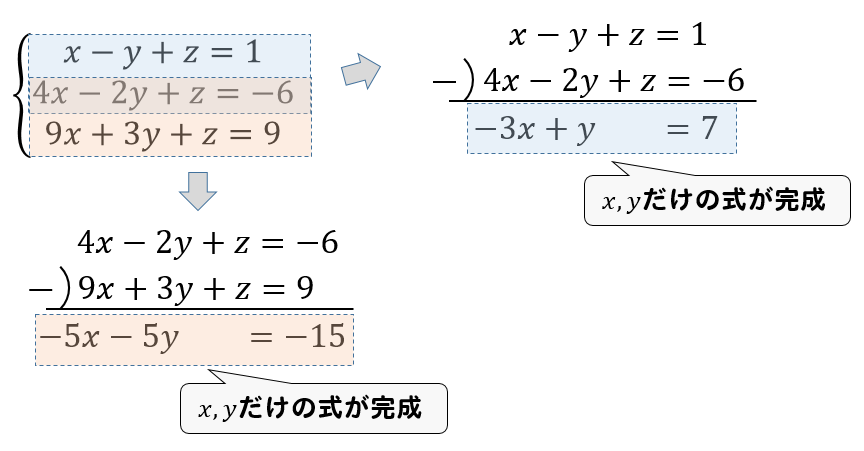連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
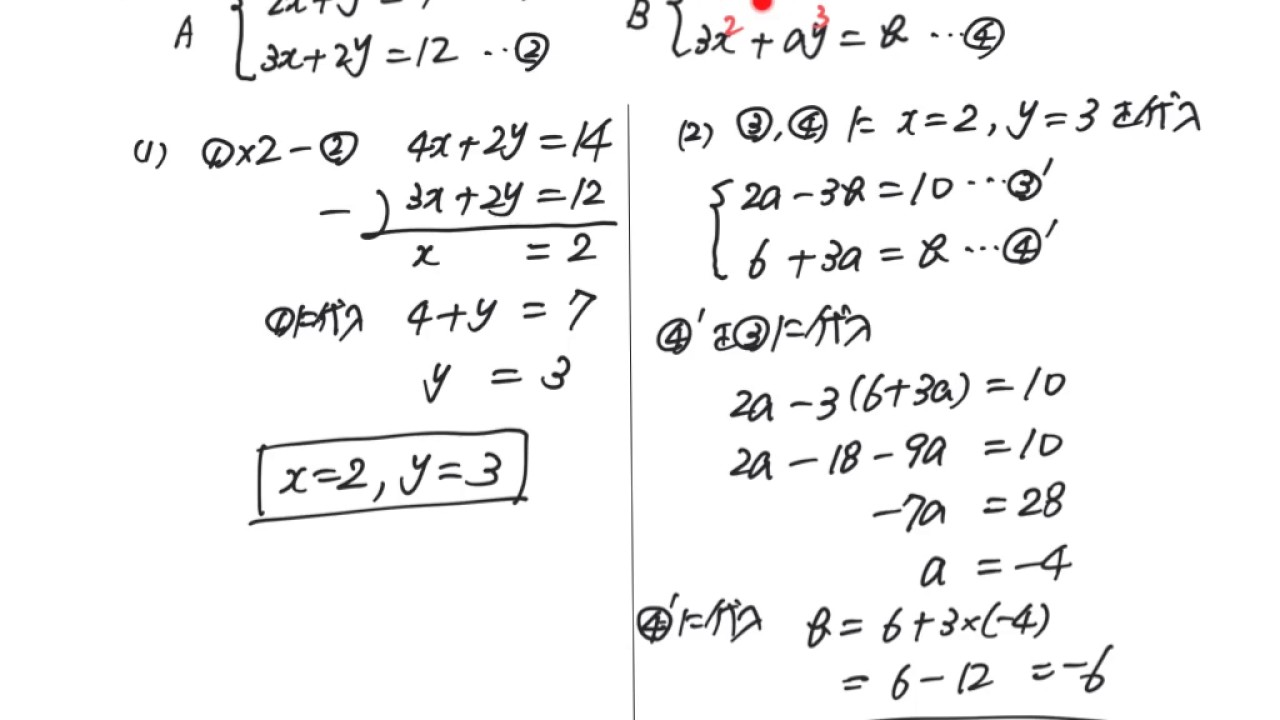連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	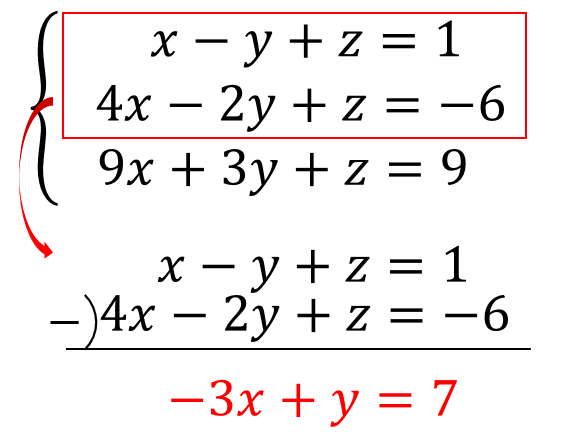連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	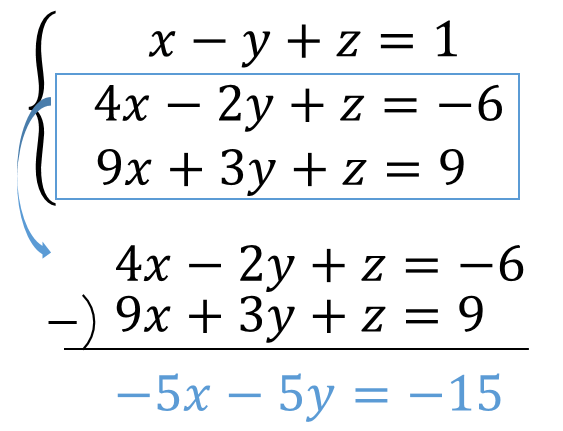連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張
連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張	連立３元１次方程式 身勝手な主張

未知数がn個 x 1, x 2, x 3, ··, x n ，方程式がn個の連立1次方程式 は，行列を用いて のように書くことができる．この連立方程式を係数行列 A を用いて A →xw = →bw と表すとき， A の逆行列 A −1 が存在すれば，連立方程式の解は次の方法で解くことができる 連立方程式「a=b=c」の解き方 次の方程式を解きなさい。 3つの式がつながっているときには、まず3つのうち2つを選んで式を作ります。 さっきとは違うペアでもう1つ式を作ります。 すると、2つ式ができたことになりますね。 ここから連立方程式を作りましょう。 ↓ あとは、この連立方程式を解いていけばOKです。 答え